分数の約分で、「九九がすぐ出てこない」という相談がありました。
九九の、全ての段の、混合の、順不同の、横式の計算は、できるそうです。
これは、素晴らしい力ですね。
以下のプリントのような、左から右へ、一方向に考えれば良い九九はすんなりできる。

これの虫食い算も、できると良いと思います。

虫食い算は、左右両方向に考えないといけないから、左から右への一方向よりも、思考が複雑です。
分子も分母も九九で割る約分は難しい
しかし、約分は難しい。
約分は、分子も分母も、九九で割らなければならない、二重の仕事だから難しいですね。
その子は、約分になると、下のプリントの(1)10分の6を、2の段で、2×1が2,2×3が6,2×4が8,2×5=10と、順につぶやいて考えているそうです。

分子も分母も、2の段で割れる!と、わかるのだからすごいと思います。
順に言って約すことが、一番の基礎なので、けなさないようにしましょう。
けなすと、脳が働かなくなり、意欲を失います。
できていることを、褒めると、自信が出て、脳が働いて、集中時間も長くなります。
大人は自分が楽にできるから、子どもにも一発解答を要求しがちです。
しかし子どもは、習得途上なので、順に言うやり方の次に、×5より大きいか小さいか予想できるようになり、年齢が上がってくると短時間で見当がつくようになります。
分数の約分は、共通の約数を脳内で考え、分子も割り、分母も割る、二重の割り算だという難しさを、大人が理解してやりましょう。
「割り算の横式が、上の段6÷2にも、下の段10÷2にもあるんだから、難しいよね。」という共感や、なぜ難しいかの言語化が大事です。
「どうしてできないの!」ではなく、どこが難しいのかを大人は考えましょう。
横式の割り算のプリントをやってみよう
横式の掛け算はできる、しかし分数の約分をすぐにできない。
横式の掛け算と、分数の約分の中間として、横式の割り算をやってみたらどうか?と考えました。


横式の割り算のプリントを90度回転してやってみよう
その後、プリントを90度回転させ、(1)は、7分の35、(2)は4分の20と式を読みます。
(1)の答えは、35に斜線\を引いて脇に5,7に斜線\を引いて脇に1と、記入します。
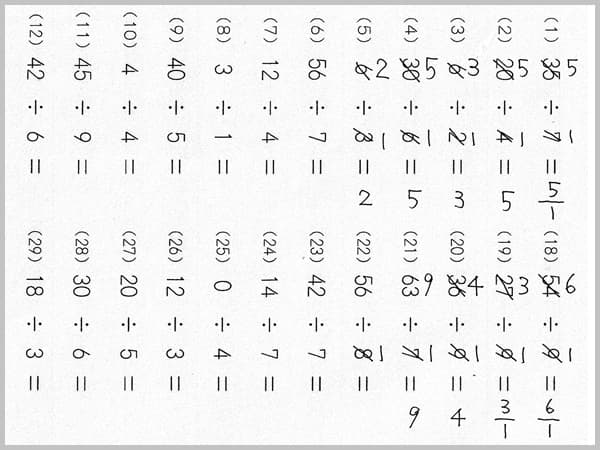
÷が、「分の」の横棒ーですね。
また、約数を目に見えるように、1,2,3,4,5,6,7,8,9の数字を、プリントの上段に書くと、良さそうです。
脳内にある約数を、脳外に数字で出して見せておくと、脳内記憶の想起負担を減らします。
約分の答えの分子や分母が2桁になる約分は難しい
約分の解答が(1)(3)(4)(14)(25)のように、1桁分の1桁になるものは、簡単です。
簡単な問題から、先にやっていい、ことを教えましょう。

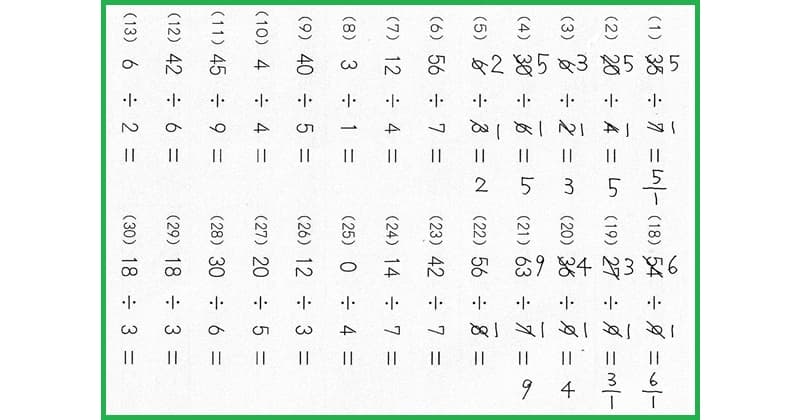
(2)(13)のように、約分の結果が、2桁の分数になる約分は難しいです。
プリントは A 4でなく A 3に拡大してメモしやすくしたり、(2)(13)のように、筆算メモの仕方を教えましょう。
たくさんあると、わからないと、イライラしやすい子どもには、1問ずつハサミで切ってやり、簡単な約分を選ばせ、簡単な約分からやらせましょう。
難しいからと取り掛からないのでなく、自分が分かりやすい問題を、探して解く力も大切です。
子どもが、どこが難しくてやる気が起きないかを、大人が説明できるようにすることで、子どもの約分を助けてみてください。
猫ちゃんブログへのコメント