教材No.31-1 お金の計数
数字と量が一致するようになると、算数加減算を学習する。
2桁以上の大きな数を学習するために、数直線も登場する。
数字と量に実感がなくても、数直線や大きな数を学習できる子どももいる。
実感がないと、その学習が難しい子には、導入にお金の数直線を使うと良い。
1円玉と10円玉と100円玉を使えば、 日常生活で見かけるお金で大きな数を実感できる。
それを計数化してやれば良い。
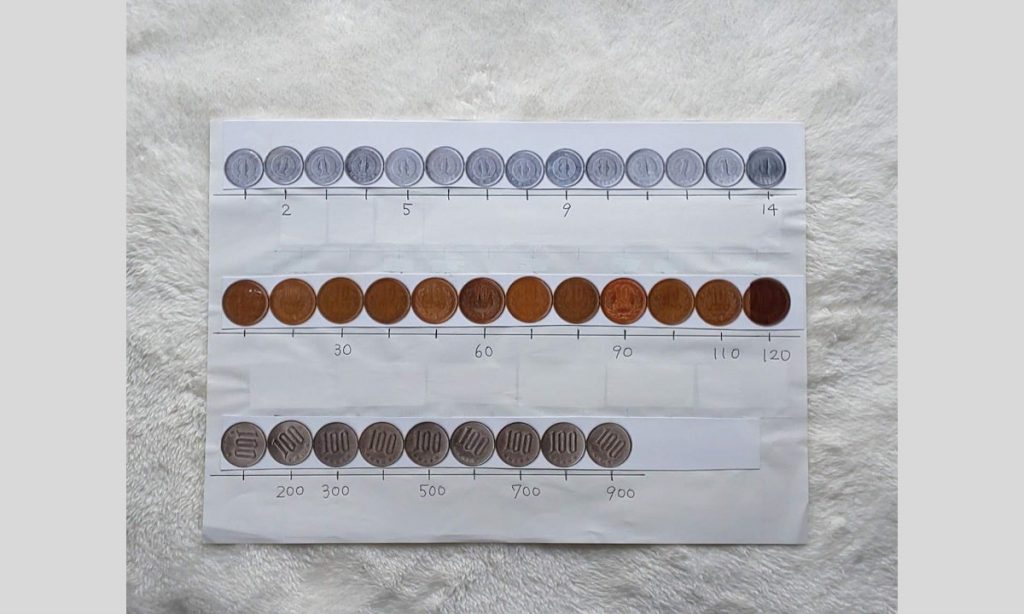
教材は、ベニヤ板か厚ボール紙と、割り箸や3 mm の角材を使って、1円玉・10円玉・100円玉の計数器を画像のように作る。

本物のお金か、おもちゃのお金を、実際におきながら、鉛筆で枠線を引き、お金のコピーをアラビックヤマト糊で張り付ける。
3mmの角材をハサミでカットして、ボンドで角材を貼り付けると良い。
一晩置くと、ピッタリと着く。
お金のコピーの表面にセロテープや透明テープを貼れば、お金を滑らす運動感覚も楽しめる。
運動とともに音声の一致も学習できる。
ベニヤや角材で枠を作るのが大変な時には、ボール紙や厚手の画用紙に、しっかりとした太マジックの黒い枠を書けば良い。
これを基礎に、プリント上に、1円玉を4枚置いたら40円、10円玉を4枚を置いたら40円を、100円玉を4枚を置いたら400円など、単一のお金で、係数が自由自在になるようにする。

数直線の穴埋め問題が難しい理由は、0の左から右方向に考えればよかった計数が、左と右の両方を考えて、間を決定しなければならないことが難しい。

そうだとすれば左から順序よく考えることを十分形成してから、左と右の2つを考えて間を決めるということを形成した方が良い。
左からの順序良い係数が出来上がっていなければ、2つの間を探すということはとてもハードルが高い。
1ずつなのか、10ずつなのか、100ずつなのか、全体の情報と部分の左右の情報を取らないと決定できない。

お金の計数機やお金のプリントを使うことによって、数直線の計数と前後の推論を形成しやすくする。
教材No.31-2 大きな数の読み取りと表記
次に異種のお金の混合で、300円、310円、312円などの読み取りと表記が自由自在になるようにする。

実物のお金の表記を離れて、プリントでも行えるようにする。
桁数や表記に混乱があれば、3円、30 円、300円、333円、330円、303円などを同時提示で学習する 。
画像は、保護者の芳野みず江さんが、息子さんの学習のために、パソコンで作成してくれたものである。
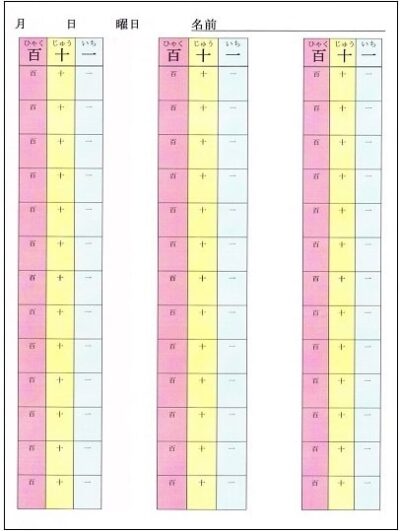
カラーで桁を意識できるようになったら、白黒プリントでも行なう。
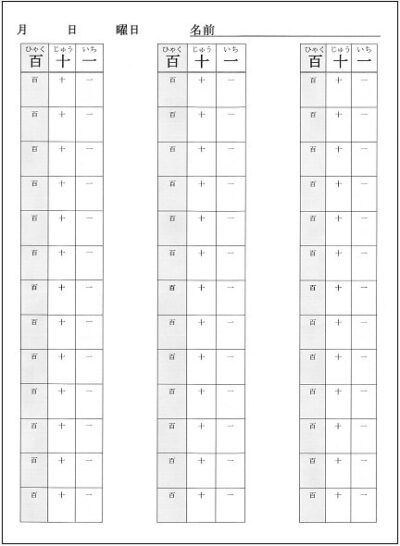
何兆何億何万何という大きな数も、枠と数字タイルで構成すると学習しやすい。

以上の学習も、初めはしっかりとした枠で行なう。
考えることに集中させるために、書く負担を減らして、数字タイルを使っておく。
枠で理解できるようになったら、仕上げをプリントで行なう。
実物に触れること、位置の記憶があること、手の運動ができることが学習を支える。
プリントに取り掛からない子がいたら、厚ボール紙にしっかりとした枠をマジックで書き、タイル数字を使って学習してみてほしい。
タイミングを見計らって、小さめの、1問のプリントを出せば、きっとやってくれる。
わかる・できると知ると、何問もある大きなプリントにも手を出すようになる。
教材No.31-2 教科書の数直線問題
最後に、教科書問題やプリント問題で練習すると良い。
渋滞するようであれば、教科書を拡大コピーして、▢の解答欄を、100までの数字タイルを使って考えると良い。
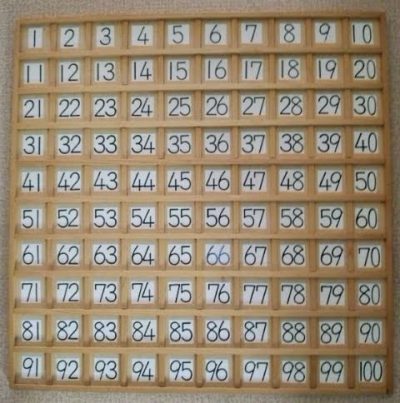
考えて決定する作業と書く作業を分けて、100までの数字タイルを使って▢の解答をすると良い。
下の画像の126頁、赤い三角6番の①②のような問題の練習がたくさんいる。
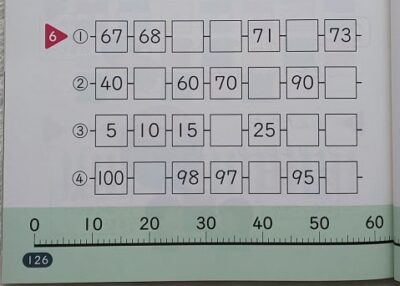
③は、5・10・15・20・25・30 の、五円玉の学習が先にいる。

④は大きな数から小さい方へ逆算していくのでとても高級だ。
教科書を180°回転させたら、左から、94・95・96・97・98・99・100と・読んだら、分かりやすいかもしれない。
順序数が分かって初めて、逆序数もわかる。
教科書問題は、スモールステップが必要な子どもの思考を、飛ばしていることが多い。
④の手前に1問、順序数94・95・96・97・98・99・100を、はさんでやると、逆序数の推論も分かりやすくなる。
猫ちゃんブログへのコメント